14. LLM Reasoning (WIP)

14.1. Introduction

Reasoning is the process in which

• a complex problem is decomposed into a sequence of smaller logical steps

• the correct execution of these logical steps leading to final soution of the problem.

In the context of LLM reasoning, it refers to the process in which LLM is generating intermediate chain of thought steps that lead to the final answer.

When we ask a question to LLM, the nature of question largely determines if a reasoning is required. For example [Fig. 14.1],

• What is the captial of China is a factual question does not require reasoning.

• A man walks at a speed of 3 mph and how har has he walked for 2 hours? is a simple reasoning problem.

• Prove there are infinitely many prime numbers is complex reasoning problem. Puzzles, riddles, coding, and math tasks are typically falling into the category of complex reasoning problems.

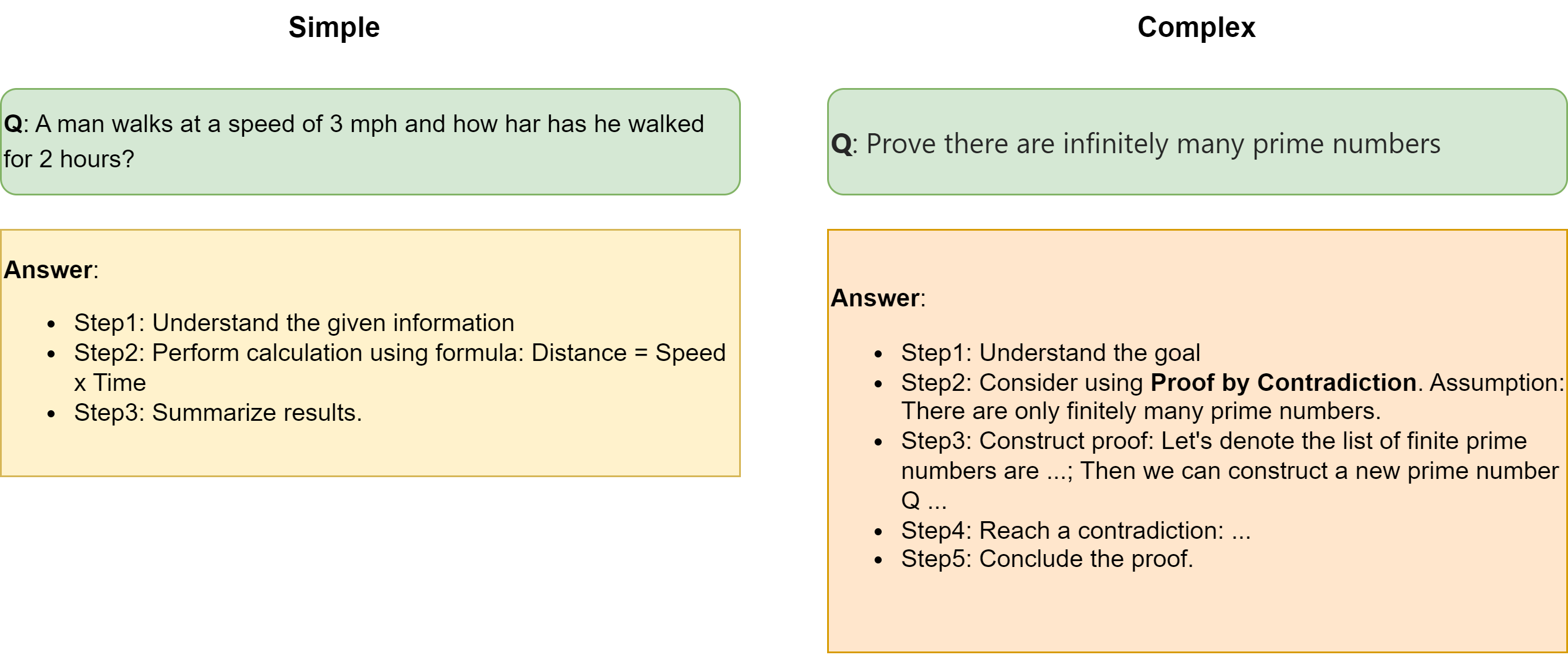
Fig. 14.1 Comparison between simple reasoning task (left) and complex reasoning task (right).

The following is a summary on simple reasoning and complex reasoning tasks from different aspects.

Aspects	Simple reasoning	Complex Reasoning
Problem Complexity	Low	High
Reasoning Steps	Few, linear	Many, linear and nonlinear, requiring planning and abstraction
Domain Knowledge	Basic or general	Often requires specialized knowledge
Example Problems	Arithmetic, factual QA, simple logic	Multi-step math, coding, and logical; plannning, optimizaiton

Most well-trained LLMs are capable of basic reasoning skill that can be triggered by CoT prompting; but they often fall short on complex reasoning benchmark. This chapter is about understanding, measuring, and developping complex reasoning skill for LLMs.

The importance of complex reasoning for LLM are:

• Better Real-World Use – Strong reasoning helps LLMs solve complex problems in fields like law, medicine, and math, making them more useful.

• Fixing Weaknesses – LLMs struggle with logical thinking and complex tasking in out-of-domain situations. Improving reasoning makes can potentially improve their generalization to new domains.

• Step Toward AGI – Reasoning is key to human intelligence. Enhancing it in LLMs moves us closer to Artificial General Intelligence (AGI).

14.2. Language, Knowledge, and Logical Reasoning benchmark

• MMLU (Measuring Massive Multitask Language Understanding) - MMLU consists of approximately 16,000 multiple-choice questions spanning 57 academic subjects, including mathematics, philosophy, law, and medicine [HBB+20]. It is widely used to assess a model’s breadth of knowledge and reasoning across diverse fields.

• GPQA (Google-Proof Q&A) - 448 multiple-choice questions written by domain experts in biology, physics, and chemistry, and requires PhD-level experts to solve.[RHS+23]. It is designed to evaluate a model’s proficiency in solving PhD-level complex problems across different domains.

• AGIEval - This includes questions from 20 official, public, and high-standard admission and qualification exams, such as the SAT, Gaokao, law school admission tests, math competitions, lawyer qualification tests, and national civil service exams [ZCG+23]. It evaluates a model’s performance on standardized tests that require advanced reasoning skills.

• ARC-AGI (Abstraction and Reasoning Corpus for Artificial General Intelligence) - RC-AGI is designed to assess a model’s abstract reasoning capabilities.t involves tasks that require pattern recognition and logical inference.

14.3. Math Benchmarks

• GSM8K (Grade School Math) - This benchmark consists of 8,500 linguistically diverse elementary school math word problems that require two to eight basic arithmetic operations to solve [CKB+21].

• MathEval - MathEval is a comprehensive benchmark (~20k problems) that contains 20 other benchmarks, such as GSM8K, MATH, and the math subsection of MMLU. It aims to evaluate the model’s math skill from elementary school math to high school competitions.

• FrontierMath - This benchmark contains questions from areas of modern math that are difficult for professional mathematicians to solve [GEB+24].

14.4. Coding Benchmark

• HumanEval - This benchmark consists of programming problems where the solution is always a Python function, often just a few lines long [CTJ+21]. This assesses a model’s basic ability to generate correct and functional code based on problem descriptions.

• SWE-Bench - The SWE-Bench comprises 2,294 software engineering problems drawn from real GitHub issues and corresponding pull requests across 12 popular Python repositories [JYW+23].

14.5. Inference-Time Scaling Strategies

Inference-time scaling refers to using more compute resources during inference, instead of training stage, to improve LLM’s ability in solving complex tasks.

Different ways for scaling test-time computing:

• Best-of-N sampling - sampling \(N\) outputs in parallel from a base LLM and take the best one (by a learned verifier or a reward model) as the final output.

• Self-critique prompting - asking the model to self-critique its response and revise its response iteratively.

• Guided search - using a process-based verifier to guide the LLM

Key findings from [SLXK24]

• For easy and intermediate questions, it is more effective to pretrain smaller models with less compute and then apply test-time compute to improve model outputs.

• With the most challenging questions, there is very little benfits from scaling-up test time compute for a smaller model; instead, it is more effective to make progress by scaling up pretraining compute .

14.5.1. Sampling and Search

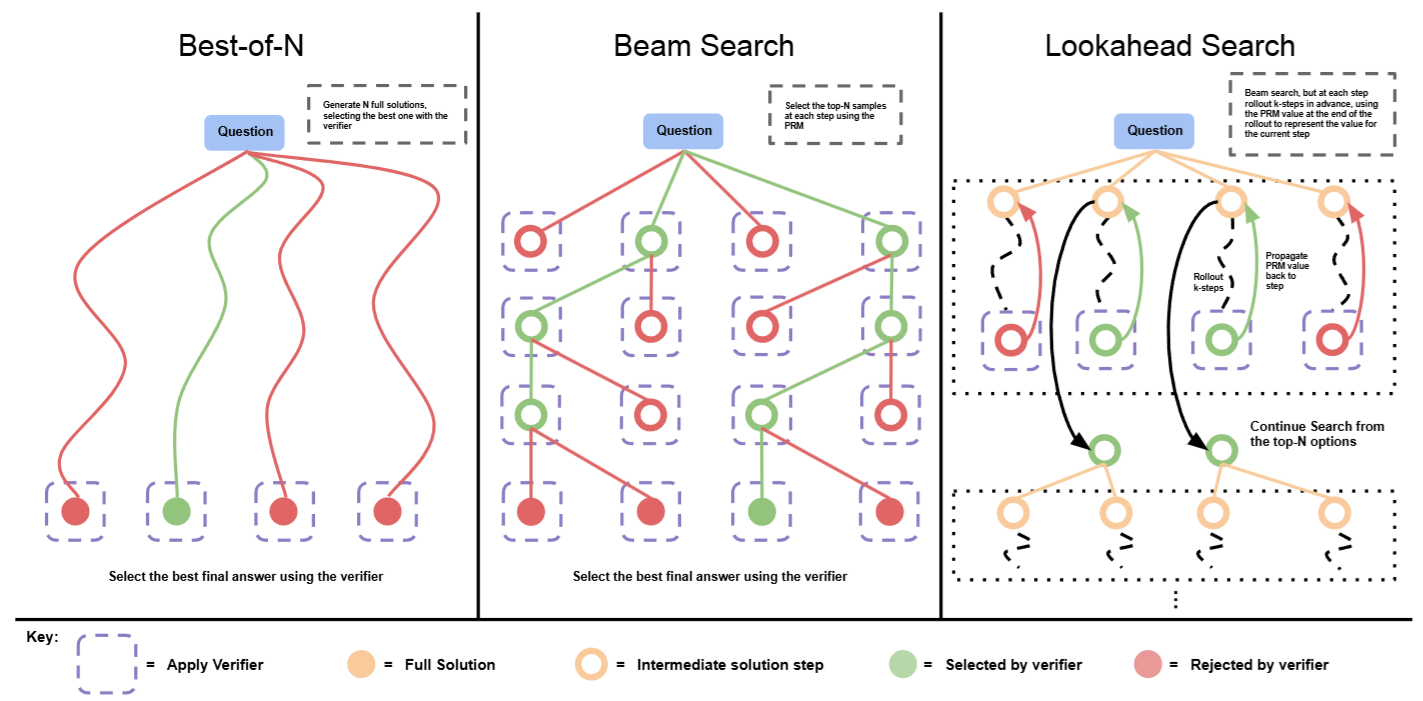
Fig. 14.2 Comparing different sampling and search methods. Left: Best-of-N samples N full answers and then selects the best answer. Center: Beam search samples N candidates at each step, and selects the top M according to the process reward model to continue the search. Right: lookahead-search extends each step in beam-search to utilize a k-step lookahead while assessing which steps to retain and continue the search. Thus lookahead-search needs more compute. Image from [SLXK24].

The most straightforward model to use inference time budget is to sample more sequence outputs and conduct search in the sequence space with the aid of scoring function. Fig. 14.2 summarizes different sampling and search methods.

The most basic sampling method is Best-of-N weighted sampling. We sample \(N\) outputs independently from an LLM and then select the best answer according to some scoring function.

Beam search. Beam search optimizes final sequence output by selecting each step guided by a process reward model (PRM). searching over its per-step predictions. Consider a fixed number of beams \(N\) and a beam width \(M\). We then run the following steps:

1. Sample \(N\) candidate tokens for the first step

2. Score the generated tokens according to the PRM’s predicted step-wise reward-to-go estimate (which also corresponds to the total reward from the existing prefix + generated token )

3. Keep for only the top \(\frac{N}{M}\) highest scoring steps

4. From each selected candidate, sample \(M\) proposals as the next step, resulting in a total of \(N / M \times M = N\) candidate prefixes again. Then repeat steps 2-4 again.

Lookahead search. Lookahead search modifies how beam search estimate the potential reward for each proposed move. It uses lookahead rollouts to improve the accuracy of the PRM’s value estimation in each step of the search process. Specifically,

• At each step in the beam search, rather than using the PRM score at the current step to select the top candidates, lookahead search performs a simulation at zero temperature.

• The Simulation involves rolling out up to \(k\) steps further while stopping early if the end of solution is reached. * The PRM’s prediction at the end of this rollout is then used to score the current step in the beam search.

Remark 14.1 (Lookahead search vs beam search vs MCTS)

Beam search can be viewed as as a special case of lookahead search with \(k=0\). Increasing \(k\) usually improve the accuracy of the per-step value estimates at the cost of additional compute, as it is closer to the final delayed reward signal.

Lookahead search can also be viewed as a special case of MCTS (Monte carlo Tree Search). MCTS has stochasticity built-in to facilitate exploration and the learning of PRM from broadly sampled sequences. Here as the focus is on exploitation of the learned PRM, so the lookahead rollout will be simulated at zero-temperature.

Authors from [SLXK24] compare the efficiency of above methods in solving reasoning problems. key findings are:

• On the easy questions, the verifier will make mostly correct assessments of correctness. Therefore, by applying beam search guided by PRM, we might overfit to any spurious features learned by the verifier, causing performance degredation.

• On the more difficult questions, the base model is much less likely to sample the correct answer in the first place, so beam search can serve to help guide the model towards producing the correct answer more often.

• With a given inference time budget, beam-search is more effective on harder questions and at lower compute budgets, whereas best-of-N is more effective on easier questions and at higher budgets (i.e., large N).

14.5.2. Proposal Distribution Refinement

One can also enable models to modify their own proposal distribution at the test time, i.e., the probability of generating \(y\) given prompt \(x\). The simplest approach is via prompting. For example, one can prompt the model to self-critique and to sequentially correct their own mistakes. However, without external feedback, directly prompting an off-the-shelf LLM to self-crique is usually ineffective for reasoning tasks [].

One approach explored by [SLXK24] is to train a model to revise their own answers iteratively, based on previous attempts at the question, therefore allowing the model to dynamically improve it’s own distribution at test time. Fig. 14.3 highlights the difference between parallel sampling approach and the sequential revision approach.

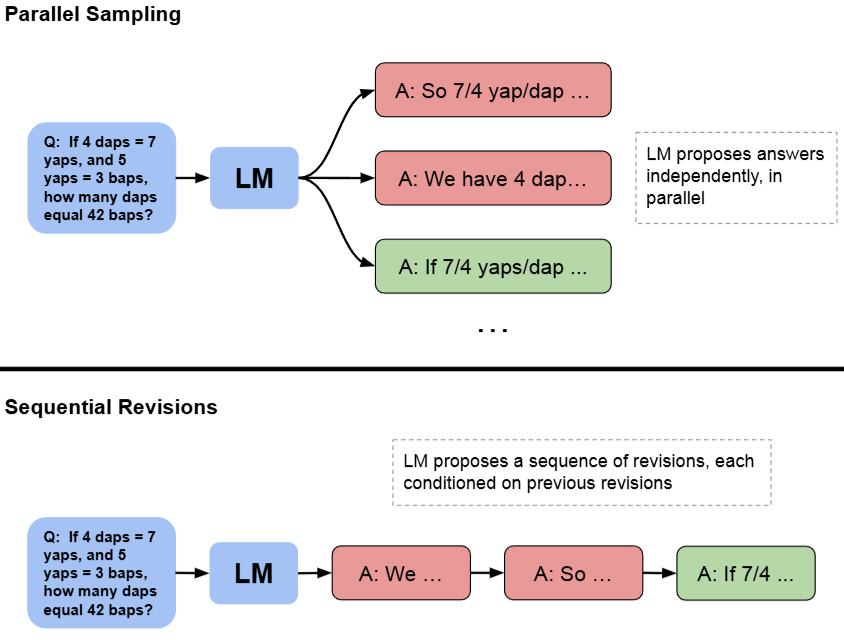
Fig. 14.3 Parallel sampling generates N answers independently in parallel, whereas sequential revisions generates each one in sequence conditioned on previous attempts. Image from [SLXK24].

Given a finetuned revision model, we can then sample a sequence of revisions from the model at test-time. Ideally, the more revision steps (thus more inference time costs), the higher chances the model can get the task correct. One can further strategically combine parallel sampling, sequential revision, and external verifier to yield a much stronger inference-time system, as shown in Fig. 14.4. To achieve best performance with given inference time budget, one needs to allocate inference time budget to each sub-component wisely.

Authors in [SLXK24] found that to best leverage the inference time budget, there exists an ideal sequential to parallel ratio, which has the dependency on problem difficulity level. In general,

• Easy questions benefit more from sequential revisions, as revision is more of local refinement.

• For difficult questions it is optimal to strike a balance between sequential and parallel computation.

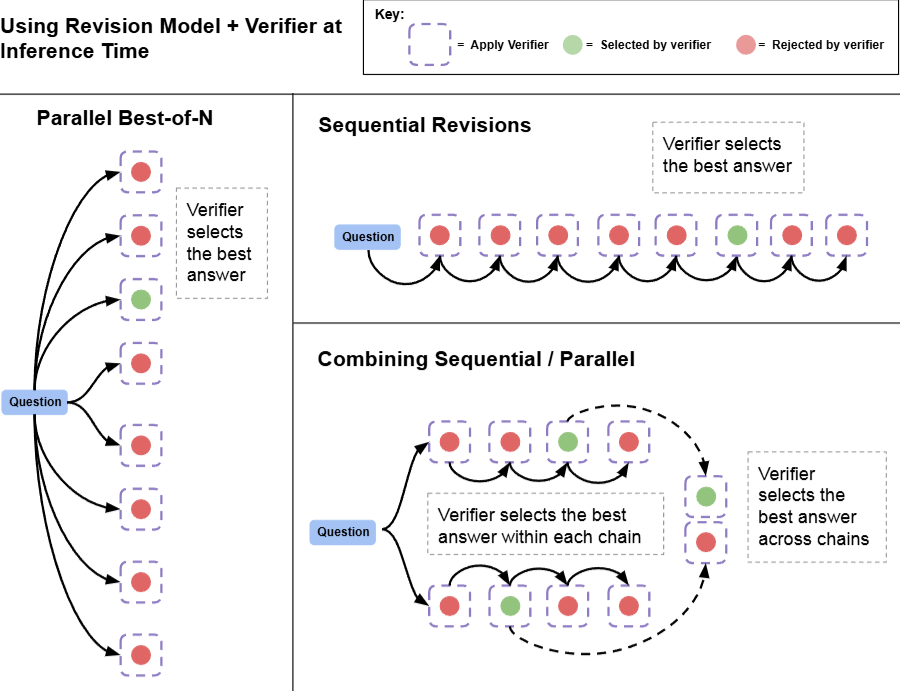
Fig. 14.4 Combining parallel sampling, sequential revision, and external verifier to yield a much stronger inference-time system. In both the sequential and parallel cases, we can use the verifier to determine the best-of-N answers. We can also allocate some of our budget to parallel and some to sequential, effectively enabling a combination of the two sampling strategies. In this case, we use the verifier to first select the best answer within each sequential chain and then select the best answer accross chains. Image from [SLXK24].

14.6. Reinfrocement Learning

14.6.1. Step-wise PPO

[WLS+23]

14.6.2. Kimi scalable RL

[TDG+25]

14.7. Preference Learning

14.7.1. Iterative RPO

Authors from [PYC+24] proposed the iterative reasoning preference optimization (iteration RPO) to enhance model’s math reasoning ability. The overview workflow is visualized in Fig. 14.5. In each iteration, there are following key steps:

• CoT and answer generation, in which thinking process and answers are generated and scored.

• Preference optimization, in which scored thinking process and answers are used to construct preference pair data and perform DPO training.

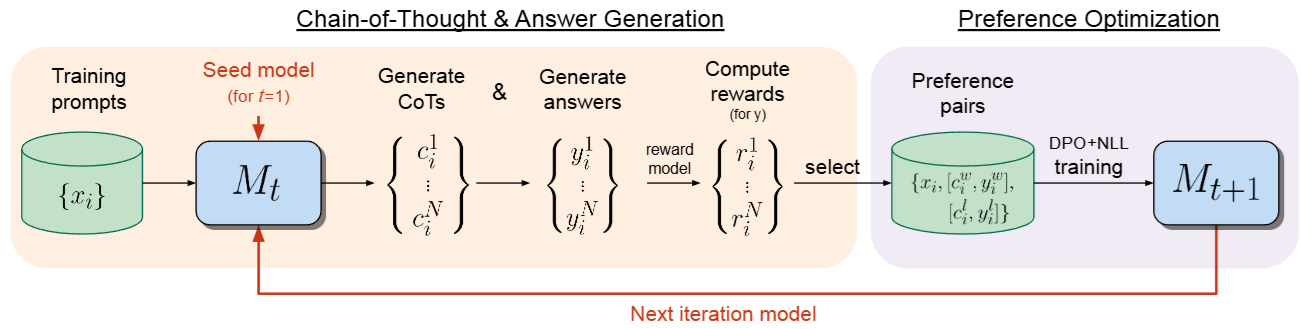
Fig. 14.5 Workflow of Iterative RPO, which consists of two steps: (i) Chain-of-Thought & Answer Generation: training prompts are used to generate candidate reasoning steps and answers from model \(M_t\), and then the answers are evaluated for correctness by a given reward model. (ii) Preference Optimization: preference pairs are selected from the generated data, which are used for training via a DPO+NLL objective, resulting in model \(M_{t+1}\). This whole procedure is then iterated resulting in improved reasoning ability on the next iteration, until performance saturates.Image from [PYC+24].

More specificially, given the current model \(M_t\), we generate \(N\) different responses for every input, where each response consists of CoT reasoning \(c\) followed by a final answer \(y\) : $\( \left(c_i^n, y_i^n\right) \sim M_t\left(x_i\right) \quad \text { for all } x_i \in D \text { and } n \in \{1,...,N\}. \)$

The reward for the response is binary - whether the prediction matches the answer.

Within the generated \(\{c_i^n, y_i^n\}\), one can group them into the winning CoT & answer and losing CoT & answer. The authors used a regularized DPO version (see DPO-Positive and Regularized DPO), with the loss function (for each pair) given by

\[ L_{DPO_R}=-\underbrace{\log \sigma\left(\beta \log \frac{M_\theta\left(c_i^w, y_i^w \mid x_i\right)}{M_t\left(c_i^w, y_i^w \mid x_i\right)}-\beta \log \frac{M_\theta\left(c_i^l, y_i^l \mid x_i\right)}{M_t\left(c_i^l, y_i^l \mid x_i\right)}\right)}_{\text{DPO}}-\alpha \underbrace{\frac{\log M_\theta\left(c_i^w, y_i^w \mid x_i\right)}{\left|c_i^w\right|+\left|y_i^w\right|}}_{\text{Regularization}} . \]

Here \(M(x)\) denotes the probability of sequence \(x\) under the current model \(M\); previous iteration’s model \(M_t\) is used as the reference model. The regularization term aims to promote the likelihood of winning sequences during the contrastive learning process.

Remark 14.2 (The importance regularization)

In math reasoning tasks, there could be cases that a minor differences on one of the multi-step reasoning process can lead to incorrect results. As discussed in DPO-Positive and Regularized DPO, when winning squencues are lexically similar to losing sequences, it require additional regularization in prevent the likelihood of winning sequences from going down.

The authors also conducted study to understand if SFT alone (without DPO) can fundamentally enhance the reasoning abilities. Their studies Fig. 14.6 show that SFT will promote the likelihood of both winning and losing sequences, which is insufficient to enhance the correct reasoning ability.

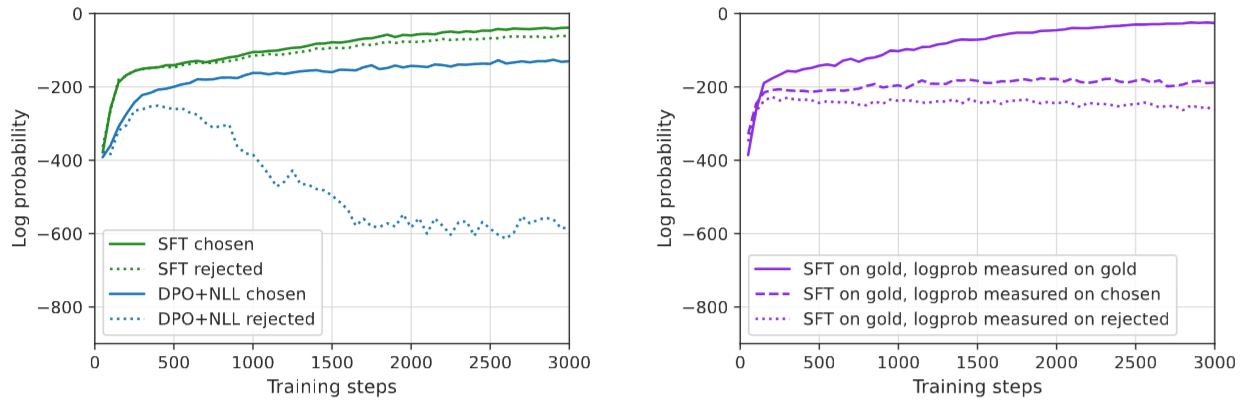
Fig. 14.6 SFT has the negative effect of promoting both chosen/positive and rejected/negative sequences, even if it is trained on gold-positive. As a comparison, DPO with regularizer loss can effectively promote chosen sequences and demote rejected sequences. Image from [PYC+24].

14.8. Bibliography

14.8.1. Software

Unsloth

[CTJ+21]

Mark Chen, Jerry Tworek, Heewoo Jun, Qiming Yuan, Henrique Ponde De Oliveira Pinto, Jared Kaplan, Harri Edwards, Yuri Burda, Nicholas Joseph, Greg Brockman, and others. Evaluating large language models trained on code. arXiv preprint arXiv:2107.03374, 2021.

[CKB+21]

Karl Cobbe, Vineet Kosaraju, Mohammad Bavarian, Mark Chen, Heewoo Jun, Lukasz Kaiser, Matthias Plappert, Jerry Tworek, Jacob Hilton, Reiichiro Nakano, and others. Training verifiers to solve math word problems. arXiv preprint arXiv:2110.14168, 2021.

[GEB+24]

Elliot Glazer, Ege Erdil, Tamay Besiroglu, Diego Chicharro, Evan Chen, Alex Gunning, Caroline Falkman Olsson, Jean-Stanislas Denain, Anson Ho, Emily de Oliveira Santos, and others. Frontiermath: a benchmark for evaluating advanced mathematical reasoning in ai. arXiv preprint arXiv:2411.04872, 2024.

[HBB+20]

Dan Hendrycks, Collin Burns, Steven Basart, Andy Zou, Mantas Mazeika, Dawn Song, and Jacob Steinhardt. Measuring massive multitask language understanding. arXiv preprint arXiv:2009.03300, 2020.

[JYW+23]

Carlos E Jimenez, John Yang, Alexander Wettig, Shunyu Yao, Kexin Pei, Ofir Press, and Karthik Narasimhan. Swe-bench: can language models resolve real-world github issues? arXiv preprint arXiv:2310.06770, 2023.

[PYC+24] (1,2,3)

Richard Yuanzhe Pang, Weizhe Yuan, Kyunghyun Cho, He He, Sainbayar Sukhbaatar, and Jason Weston. Iterative reasoning preference optimization. arXiv preprint arXiv:2404.19733, 2024.

[RHS+23]

David Rein, Betty Li Hou, Asa Cooper Stickland, Jackson Petty, Richard Yuanzhe Pang, Julien Dirani, Julian Michael, and Samuel R Bowman. Gpqa: a graduate-level google-proof q&a benchmark. arXiv preprint arXiv:2311.12022, 2023.

[SLXK24] (1,2,3,4,5,6,7)

Charlie Snell, Jaehoon Lee, Kelvin Xu, and Aviral Kumar. Scaling llm test-time compute optimally can be more effective than scaling model parameters. arXiv preprint arXiv:2408.03314, 2024.

[TDG+25]

Kimi Team, Angang Du, Bofei Gao, Bowei Xing, Changjiu Jiang, Cheng Chen, Cheng Li, Chenjun Xiao, Chenzhuang Du, Chonghua Liao, and others. Kimi k1. 5: scaling reinforcement learning with llms. arXiv preprint arXiv:2501.12599, 2025.

[WLS+23]

Peiyi Wang, Lei Li, Zhihong Shao, RX Xu, Damai Dai, Yifei Li, Deli Chen, Y Wu, and Zhifang Sui. Math-shepherd: a label-free step-by-step verifier for llms in mathematical reasoning. arXiv preprint arXiv:2312.08935, 2023.

[ZCG+23]

Wanjun Zhong, Ruixiang Cui, Yiduo Guo, Yaobo Liang, Shuai Lu, Yanlin Wang, Amin Saied, Weizhu Chen, and Nan Duan. Agieval: a human-centric benchmark for evaluating foundation models. arXiv preprint arXiv:2304.06364, 2023.