3. Early Neural Language Models#
3.1. Motivation#
As we mentioned above, \(n\)-gram models are count based methods, aimming to learn the joint distribution of word sequences, with the key assumption that the probability of a word depends only on the n-1 words that precede it.
It has challenges in language modeling from the following aspects:
Curse of dimensionality when \(n\) becomes large. For example, consider a language with a vocabulary of size \(V = 10^6\), a 10-gram model would require model parameters of \(V^{10}\).
Difficulty in modeling long sequence dependency due to the sparsity of the long sequencenes data as well as the curse of dimensionaltiy for large \(n\).
Inaccuracy in modeling sequences containing rare words, although we can apply smoothing functions to alleviate the difficulty.
Poor genearlization to unseen word combination.
The recent neural language models are good at capturing the semantics of words, and they give good prediction for low frequency sequences.
These limitations of \(n\)-gram models motivated researchers to explore neural network approaches [[BDVJ03, MKB+10]] that could capture deeper semantic relationships and longer-range dependencies in language. The resulting neural language models are proved to have the following advantages
Improved efficient representation: Neural networks can learn a compact distributed representations of words (word embeddings), capturing semantic similarities. As a comparison, n-gram model only stores the statistical counting results.
Better generalization with efficient model parameters: Neural models can generalize to unseen word combinations more effectively.
Handling longer contexts: Recurrent neural network architectures allow for theoretically unlimited context.
3.1.1. Feed-forward Neural Language Model#
The core idea of \(n\)-gram model is nothing but a mechanical counter of co-occurrence of words. In natural language, there are many words that are similar in their meaning as wells as their grammar rules. For example, A cat is walking in the living room vs. a dog is running in the bedroom have similar word pairs (cat, dog), (walking, running), (living room, bedroom) and use similar patterns. These similarities or word semantic meaning (i.e., the latent representation of words) can be exploited to construct model with much smaller model parameters.
[BDVJ03] proposed neural language models, which predict and generate next word based on its context and operating at a low dimensional dense vector space (i.e., word embedding).
The core idea is that by projecting words into low dimensional space (via learning and gradient descent), words with similar semantics are automatically clustered together, thus providing opportunities for effecient parameterization and mitigating the the curse of dimensionality in \(n\)-gram language models.
In the feed-forward network model, each word, together with its preceding \(n - 1\) words as context are projected into low-dimensional space and further predict the next word probability. Note that the context has a fixed length of \(n\), which it is limited in the same way as in \(n\)-gram models [chapter_foundation_fig_language_model_feedforward_model].
Formally, the model is optimized to maximize
The \(y_{i}\) is the logic for word \(i\), given by
where \(W, H\) are matrices and \(b, d\) are biases. Here \(W\) can optionally zero, meaning no direct connections. \(e = (e_1,...,e_{n-1})\) is the concatenations of word embeddings of each preceding token.
Feed-forward neural language model brings several improvements over the traditional \(n\)-gram language model: it provides a compact and efficient parameterization to capture word dependencies among text data. Recall that \(n\)-gram model would have to store all observed \(n\)-grams. However, feed-forward neural language model still meet challenges to capture long-distance dependencies in natural language. In the feed-forward neural language model, capturing long-distance dependencies will require an increase of the context window size, which linearly scales with model parameters \(W\). Another drawback is that a word that appears at different locations will be multiplied by different weights to get its embedding, which is inconsistent.
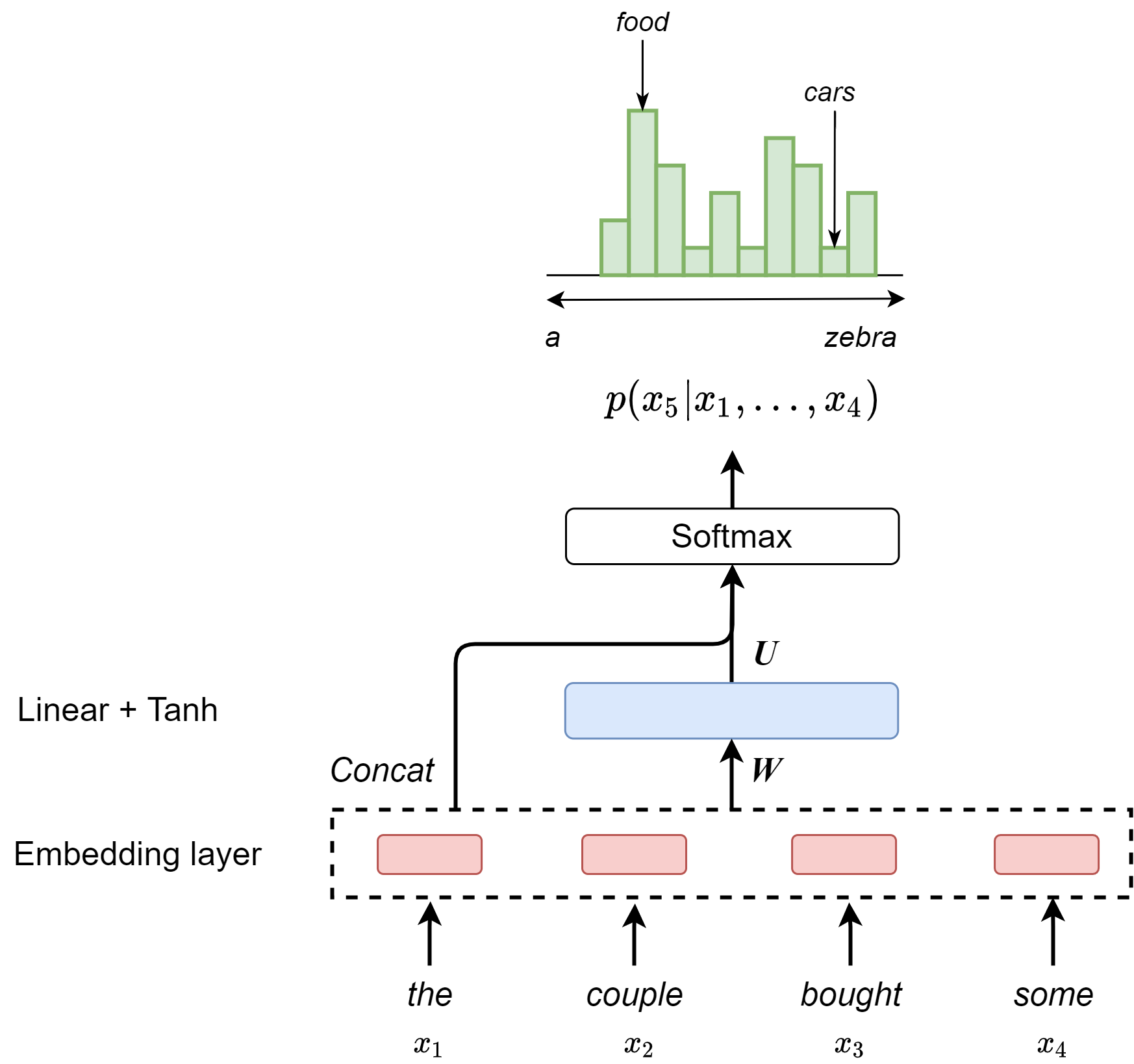
Fig. 3.1 Feedforward neural netowk based language model.#
3.2. Recurrent Neural Language Model#
In recurrent network model [Fig. 3.2], context modeling ability is extended via recurrent connections and context modeling length is theoretically unlimited. Specially, let the recurrent network input be \(x\), hidden layer output be \(h\) and output probabilities be \(y\). Input vector \(x_t\) is a concatenation of a word vector \(w_t\) and the previous hidden layer output \(s_{t-1}\), which represents the context. To summarize, we have recurrent computation given by
The prediction probability at each \(t\) is given by
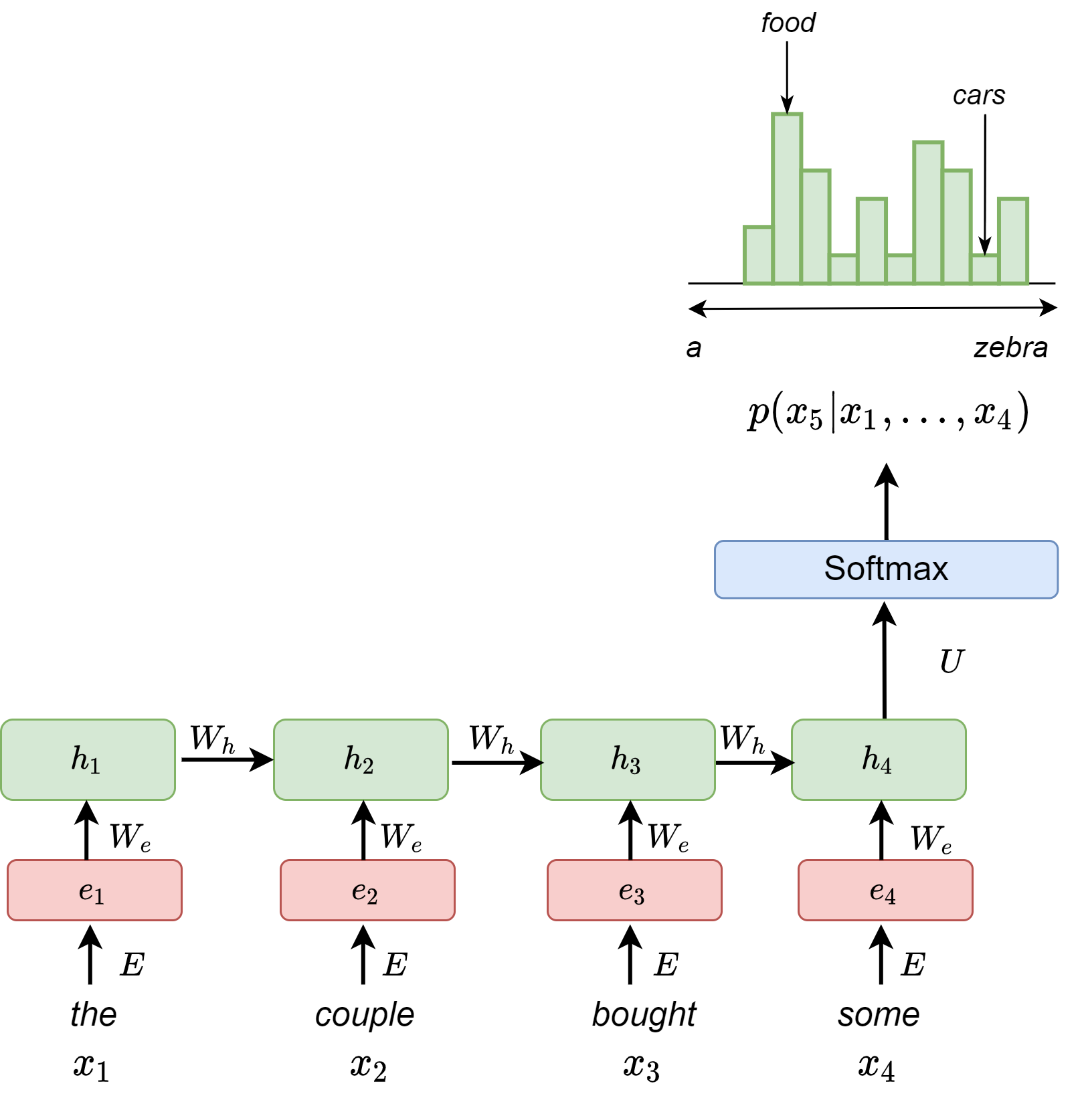
Fig. 3.2 Recurrent neural network based language model.#
Compared with \(n\)-gram language model and feed-forward neural language model, **RNN language model can in principle process input of any length without increasing the model size. **
RNN language model also has several drawbacks: Computing a conditional probability \(p(w_t|w_{1:t-1})\) is expensive. One mitigating strategy is to cache and re-use previous computed results or to pre-compute conditional probabilities for frequent \(n\)-grams.
3.3. Bibliography#
Yoshua Bengio, Réjean Ducharme, Pascal Vincent, and Christian Jauvin. A neural probabilistic language model. Journal of machine learning research, 3(Feb):1137–1155, 2003.
Tomas Mikolov, Martin Karafiát, Lukás Burget, Jan Cernocký, and Sanjeev Khudanpur. Recurrent neural network based language model. In Takao Kobayashi, Keikichi Hirose, and Satoshi Nakamura, editors, INTERSPEECH, 1045–1048. ISCA, 2010. URL: http://dblp.uni-trier.de/db/conf/interspeech/interspeech2010.html#MikolovKBCK10.
