10. MoE Sparse Architectures (WIP)

10.1. MoE architecture fundamentals

10.1.1. Motivation

The MoE architecture is a type of neural network design that employs multiple experts to solve complex problems. It incorporates multiple specialized networks, called experts, each trained to handle a specific aspect of the data or task. A gating network acts as a router, dynamically routing input data to the most relevant expert(s) for processing. This selective activation of experts leads to sparse activation, where only a subset of the model’s parameters are actively engaged at any given time, resulting in improved efficiency and reduced computational cost .

The LLM scaling law indicates that larger models lead to better results - given a fixed computing budget, training a larger model for fewer steps is better than training a smaller model for more steps.

Due to their sparse activation characteristics, MoE models can be pretrained with significantly less computational resources. This allows for substantial scaling of the model or dataset size within the same compute budget as a dense model. Specifically, an MoE model can achieve the same quality during pretraining compared to its dense counterpart.

10.1.2. Key Componenents

The MoE architecture differentiate from dense architecture from the following two key components [Fig. 10.1]:

Experts: These are individual neural networks, each specializing in a particular domain or aspect of the problem. The number of experts can vary depending on the model’s complexity and the diversity of the data. In practice, each expert is a FFN.

Gating Network: This network acts as a router, evaluating the input data and determining which expert(s) are best suited to process it. The gating network assigns weights to each expert, indicating its contribution to the final output. The gating function \(G\) used in MoE is typically Softmax, which assigns probabilities to each expert based on the input \(x\). More specifically,

\[\begin{split} \begin{align*} y&=\sum_{i=1}^n G(x)_i E_i(x) \\ G&=\operatorname{Softmax}\left(x \cdot W_g\right) \end{align*}. \end{split}\]

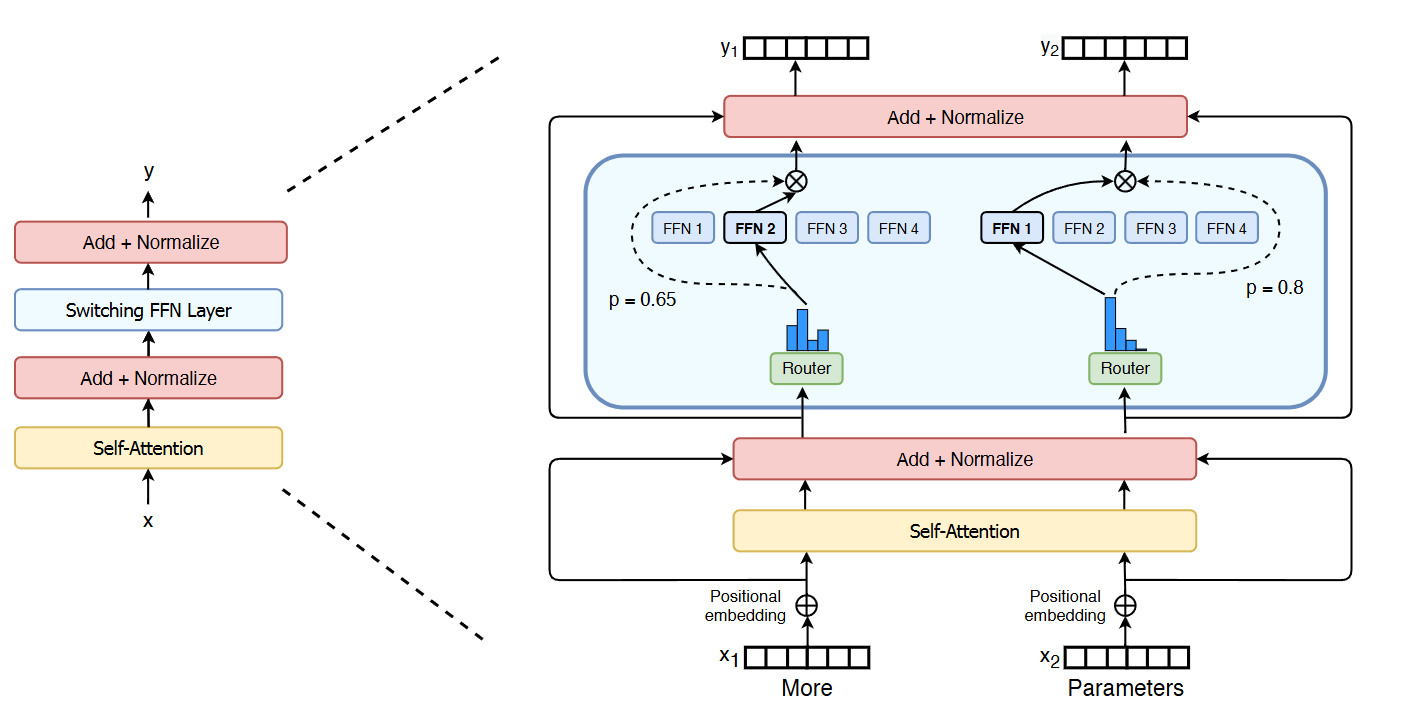
Fig. 10.1 Illustration of a Switch Transformer encoder block. The FFN layer becomes a sparse Switch FFN layer (light blue), which operates independently on the tokens in the sequence. The Switch FFN layer consists of four FFN experts. The router independently route each token and activate a subset of FFN experts with different probabilities. Image from [FZS22]

When an input is presented to the MoE model, the gating network analyzes it and selects the most appropriate expert(s) based on their expertise. The input is then processed by the chosen experts, and their outputs are combined using the weights assigned by the gating network to produce the final output. A crucial aspect of MoE functionality is the loss function, which is designed to optimize both the individual experts and the gating network, ensuring efficient collaboration and accurate results.

10.1.3. Load Balancing

In MoEs models, the gating network is responsible for distributing input data to different experts [Fig. 10.2]. However, this distribution can become uneven, leading to a load imbalance challenge. This means some experts might be overloaded with data while others remain idle. This imbalance can hinder the model’s performance and efficiency.

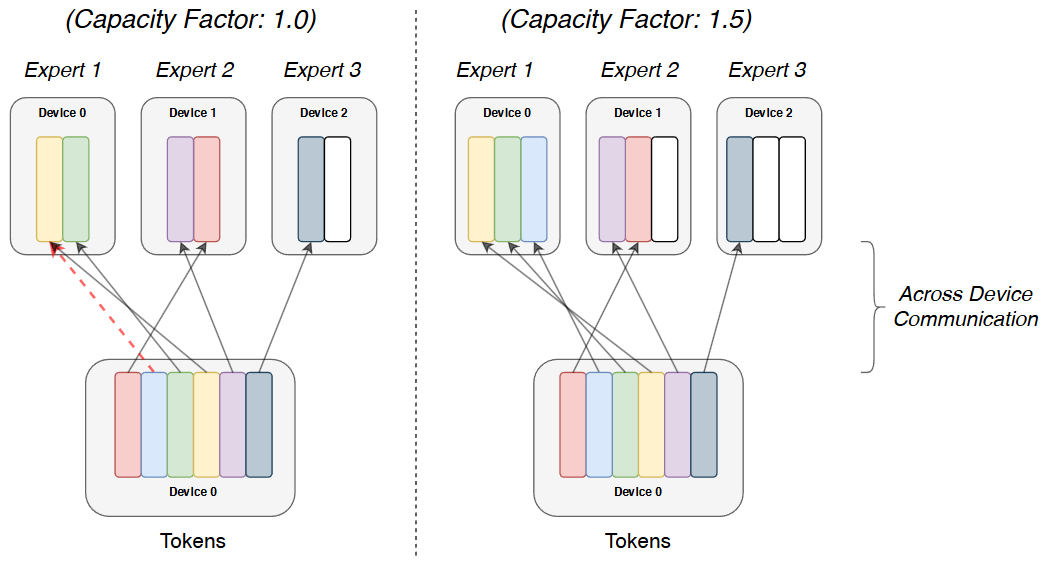
Fig. 10.2 Illustration of token routing dynamics for MoE architecture. Each token is routed to the expert with the highest router probability. Image from [FZS22]

Note that each expert has a fixed capacity given by

\[\operatorname{Capacity} = (\text{total tokens} / \text{num experts}) \times \text{capacity factor}\]

If the tokens are unevenly dispatched then certain experts will overflow, resulting in these tokens not being processed by this layer. Setting a larger capacity factor alleviates this overflow issue, but also increases computation and communication costs.

In summary, key problems associated with load imbalance:

• Token dropping: Some tokens might not be processed by any expert due capacity limit, leading to information loss.

• Model collapse: Most tokens might be routed to only a few experts, effectively reducing the model’s capacity and hindering its ability to learn diverse patterns.

To address this challenge, researchers have developed various load balancing solutions. These solutions aim to ensure a more even distribution of tokens among experts, improving the model’s overall performance and efficiency.

• Auxiliary Loss: This method introduces an additional loss term during training that penalizes uneven expert utilization. This encourages the gating network to distribute tokens more evenly.

• **Loss-Free Balancing:**This approach include

  • Dynamically adjusts expert biases based on their recent load without relying on auxiliary losses.

  • Iteratively adjusts routing probabilities to achieve a more balanced distribution of tokens.

  • Exchanging experts between different devices or nodes in a distributed training setup to balance the load.

These solutions aim to mitigate the load imbalance challenge in MoE models, ensuring that all experts are effectively utilized and contribute to the model’s overall performance. As research in this area continues, we can expect further advancements in load balancing techniques, leading to more efficient and robust MoE models.

10.1.4. MoE vs Dense Model

Feature	MoE	Dense
Structure	Multiple experts and a gating network	Fully connected layers
Functionality	Selective activation of experts based on input	Sequential processing of data through all layers
Scalability	More scalable due to sparse activation	Less scalable due to computational cost
Efficiency	More efficient due to reduced computation	Less efficient due to processing all parameters
Specialization	Experts specialize in specific domains	All neurons contribute to general understanding
Complexity	More complex to implement and train	Simpler to implement and train
Memory Requirement	High memory requirements to load all experts	Moderate memory requirements

Example MoE Models

Name	Details
Mixtral	sparse mixture of 8 7B-experts; total model parameters 47B
DeepSeek V3	sparse mixture of 24? 37B-experts; total model parameters 671B

As shown in the Mixtral Fig. 10.3, MoE can provide better efficiency-cost trade-off and achieve much better performance compared to dense model (e.g., llama2) of the same size.

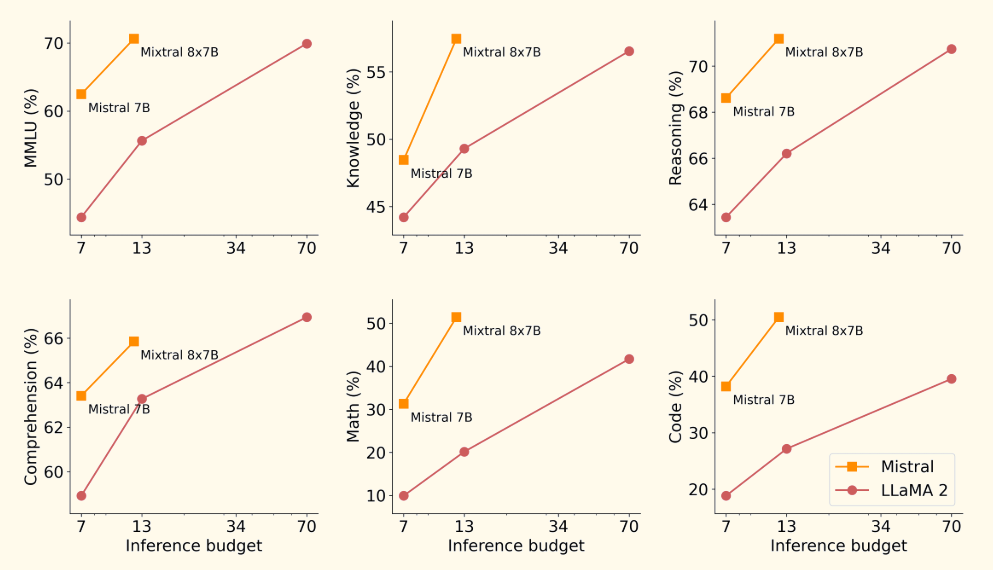
Fig. 10.3 Comparison of performance vs efficiency trade-off between Mistral-7B/Mixtral-8x7b and Llama 2 models (7B, 13B, 70B) on different tasks. Image source.

10.2. Switch Transformer

10.2.1. Load Balancing Loss

To encourage a balanced load across experts we add an auxiliary loss. For each Switch layer, this auxiliary loss is added to the total model loss during training. Given \(N\) experts indexed by \(i=1\) to \(N\) and a batch \(\mathcal{B}\) with \(T\) tokens, the auxiliary loss is computed as the scaled dot-product between vectors \(f\) and \(P\),

\[ \operatorname{loss}=\alpha \cdot N \cdot \sum_{i=1}^N f_i \cdot P_i \]

where \(f_i\) is the fraction of tokens dispatched to expert \(i\),

\[ f_i=\frac{1}{T} \sum_{x \in \mathcal{B}} \mathbb{1}\{\operatorname{argmax} p(x)=i\} \]

and \(P_i\) is the fraction of the router probability allocated for expert \(i,{ }^2\)

\[ P_i=\frac{1}{T} \sum_{x \in \mathcal{B}} p_i(x) \]

Since we seek uniform routing of the batch of tokens across the \(N\) experts, we desire both vectors to have values of \(1 / N\). The auxiliary loss of encourages uniform routing since it is minimized under a uniform distribution.

Note that the strength parameter \(\alpha\) needs careful tuning - too large an auxiliary loss can disturb the normal gradient and eventually impair the model performance.

10.3. DeepSeek MoE

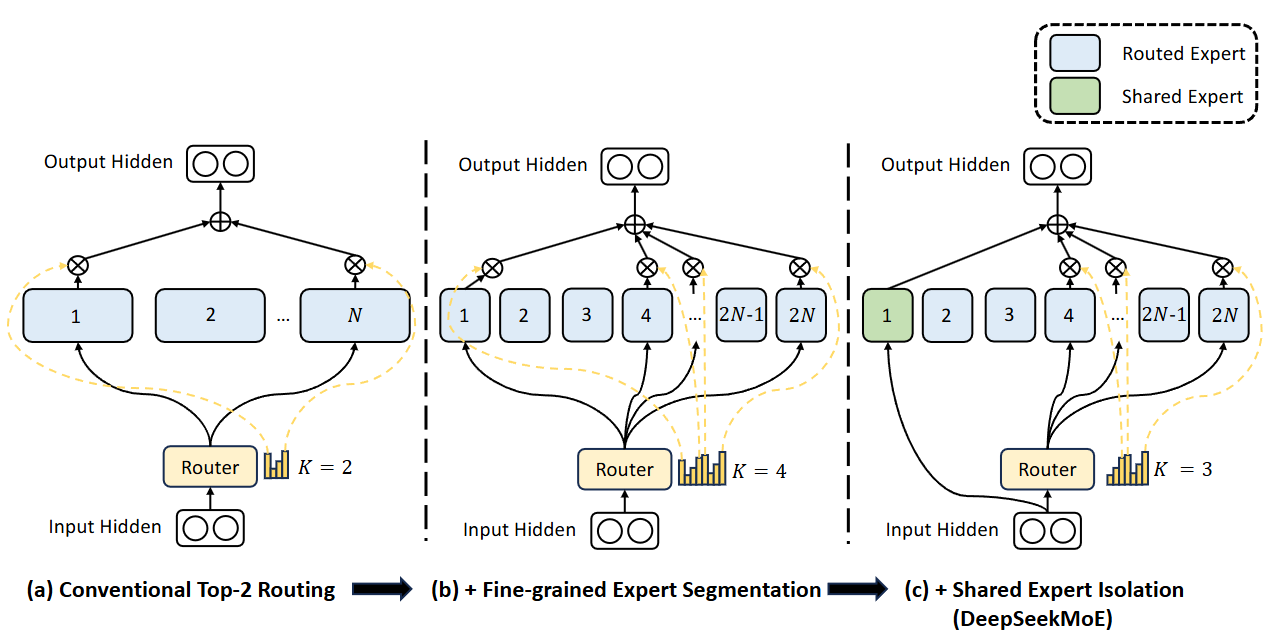
Fig. 10.4 Illustration of a Switch Transformer encoder block. The FFN layer becomes a sparse Switch FFN layer (light blue), which operates independently on the tokens in the sequence. The Switch FFN layer consists of four FFN experts. The router independently route each token and activate a subset of FFN experts with different probabilities. Image from [DDZ+24]

10.3.1. Load Balance Consideration

Two level of load balance strategies are considered in DeepSeek-MoE:

• Expert-level balance, which encourages that every expert to receive sufficient tokens and training.

• Device-level balance, which ensure every device (i.e., each device has multiple experts in distributed training) to have balanced computational load, therefore alleviating computation bottlenecks.

The expert-level balance is realized via the expert-level balance loss, given as follows:

\[\begin{split} \begin{aligned} \mathcal{L}_{\text {ExpBal }} & =\alpha_1 \sum_{i=1}^{N^{\prime}} f_i P_i \\ f_i & =\frac{N^{\prime}}{K^{\prime} T} \sum_{t=1}^T \mathbb{1}(\text { Token } t \text { selects Expert } i), \\ P_i & =\frac{1}{T} \sum_{t=1}^T s_{i, t} \end{aligned} \end{split}\]

where \(\alpha_1\) is a hyper-parameter called expert-level balance factor, \(N^{\prime}\) is equal to ( \(m N-K_s\) ) and \(K^{\prime}\) is equal to ( \(m K-K_s\) ) for brevity. \(\mathbb{1}(\cdot)\) denotes the indicator function.

Similarly, for device-level balance, if we partition all routed experts into \(D\) groups, and deploy each group on a single device, the device-level balance loss is computed as follows:

\[ \mathcal{L}_{\text {DevBal }} & =\alpha_2 \sum_{i=1}^D f_i^{\prime} P_i^{\prime} \]

where

• \(\alpha_2\) is a hyper-parameter called device-level balance factor.

• \(f_i^{\prime} =\frac{1}{\left|\mathcal{E}_i\right|} \sum_{j \in \mathcal{E}_i} f_j\), Experts are assigned to devices denoted by \(\left\{\mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_D\right\}\)

• P_i^{\prime} & =\sum_{j \in \mathcal{E}_i} P_j

In practice, we set a small expert-level balance factor to mitigate the risk of routing collapse, and meanwhile set a larger device-level balance factor to promote balanced computation across the devices.

10.4. DeepSeek V3

10.4.1. Overview

DeepSeek-V3 [DALF+24] is a powerful Mixture-of-Experts (MoE) language model with 671 billion total parameters, of which 37 billion are activated for each token. This model builds upon the successes of its predecessor, DeepSeek-V2, by incorporating several architectural and training innovations to achieve state-of-the-art performance with remarkable efficiency.

The key elements are:

• Multi-head Latent Attention (MLA): This mechanism reduces the computational complexity of attention by projecting keys and values into a lower-dimensional latent space.

• DeepSeekMoE: This architecture enhances MoE by incorporating techniques like expert choice routing and grouped query attention to improve efficiency and load balancing.

• Auxiliary-loss-free Load Balancing: DeepSeek-V3 introduces a novel approach to load balancing that avoids the use of auxiliary losses, which can interfere with training and hinder performance. This strategy dynamically adjusts expert biases based on their recent load to ensure a more even distribution of tokens.

• Multi-token Prediction (MTP): This training objective encourages the model to predict multiple tokens simultaneously, leading to improved performance and enabling faster inference through speculative decoding.

10.4.2. Architecture

In response to the aforementioned issues, we introduce DeepSeekMoE, an innovative MoE architecture specifically designed towards ultimate expert specialization. Our architecture involves two principal strategies:

• Fine-Grained Expert Segmentation: while maintaining the number of parameters constant, we segment the experts into a finer grain by splitting the FFN intermediate hidden dimension. Correspondingly, keeping a constant computational cost, we also activate more fine-grained experts to enable a more flexible and adaptable combination of activated experts. Fine-grained expert segmentation allows diverse knowledge to be decomposed more finely and be learned more precisely into different experts, where each expert will retain a higher level of specialization. In addition, the increased flexibility in combining activated experts also contributes to a more accurate and targeted knowledge acquisition.

• Shared Expert Isolation: we isolate certain experts to serve as shared experts that are always activated, aiming at capturing and consolidating common knowledge across varying contexts. Through compressing common knowledge into these shared experts, redundancy among other routed experts will be mitigated. This can enhance the parameter efficiency and ensure that each routed expert retains specialized by focusing on distinctive aspects. These architectural innovations in DeepSeekMoE offer opportunities to train a parameter-efficient MoE language model where each expert is highly specialized.

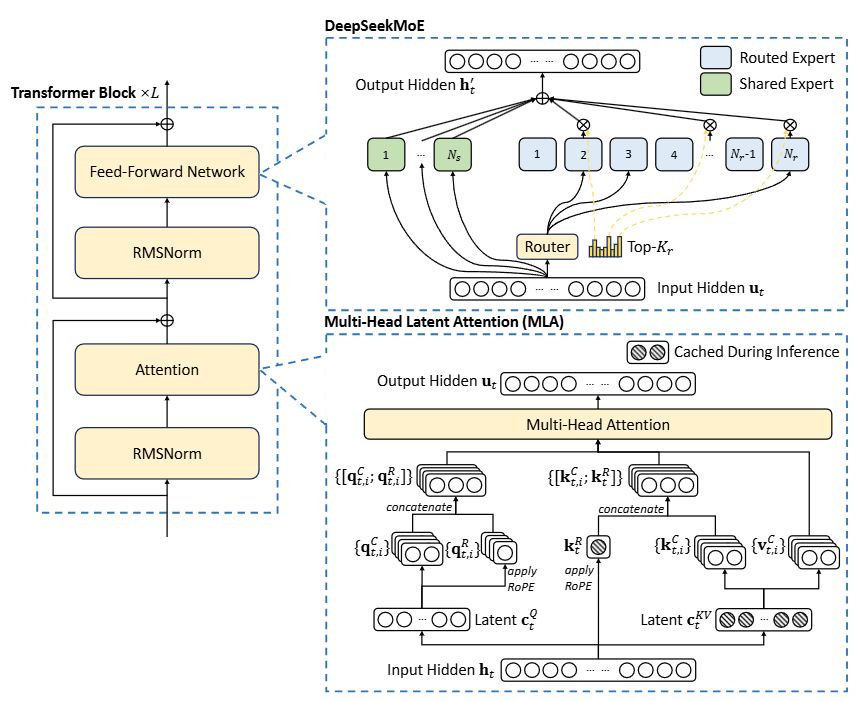
Fig. 10.5 Illustration of a Switch Transformer encoder block. The FFN layer becomes a sparse Switch FFN layer (light blue), which operates independently on the tokens in the sequence. The Switch FFN layer consists of four FFN experts. The router independently route each token and activate a subset of FFN experts with different probabilities. Image from [DALF+24]

Towards this objective, in addition to the fine-grained expert segmentation strategy, we further isolate \(K_s\) experts to serve as shared experts. Regardless of the router module, each token will be deterministically assigned to these shared experts. In order to maintain a constant computational cost, the number of activated experts among the other routed experts will be decreased by \(K_s\), as depicted in Figure 2(c). With the shared expert isolation strategy integrated, an MoE layer in the complete DeepSeekMoE architecture is formulated as follows:

\[\begin{split} \begin{aligned} & \mathbf{h}_t^l=\sum_{i=1}^{K_s} \operatorname{FFN}_i\left(\mathbf{u}_t^l\right)+\sum_{i=K_s+1}^{m N}\left(g_{i, t} \operatorname{FFN}_i\left(\mathbf{u}_t^l\right)\right)+\mathbf{u}_t^l, \\ & g_{i, t}= \begin{cases}s_{i, t}, & s_{i, t} \in \operatorname{Topk}\left(\left\{s_{j, t} \mid K_s+1 \leqslant j \leqslant m N\right\}, m K-K_s\right), \\ 0, & \text { otherwise },\end{cases} \\ & s_{i, t}=\operatorname{Softmax}_i\left(\mathbf{u}_t^{l^T} \mathbf{e}_i^l\right) \end{aligned} \end{split}\]

Finally, in DeepSeekMoE, the number of shared expert is \(K_s\), the total number of routed experts is \(m N-K_s\), and the number of nonzero gates is \(m K-K_s\).

10.4.3. Loss-Free Load Balanace

To achieve a better trade-off between load balance and model performance, we pioneer an auxiliary-loss-free load balancing strategy (Wang et al., 2024a) to ensure load balance. To be specific, we introduce a bias term \(b_i\) for each expert and add it to the corresponding affinity scores \(s_{i, t}\) to determine the top-K routing:

\[\begin{split} g_{i, t}^{\prime}= \begin{cases}s_{i, t}, & s_{i, t}+b_i \in \operatorname{Topk}\left(\left\{s_{j, t}+b_j \mid 1 \leqslant j \leqslant N_r\right\}, K_r\right) \\ 0, & \text { otherwise }\end{cases} \end{split}\]

Note that the bias term is only used for routing. The gating value, which will be multiplied with the FFN output, is still derived from the original affinity score \(s_{i, t}\). During training, we keep monitoring the expert load on the whole batch of each training step. At the end of each step, we will decrease the bias term by \(\gamma\) if its corresponding expert is overloaded, and increase it by \(\gamma\) if its corresponding expert is underloaded, where \(\gamma\) is a hyper-parameter called bias update speed. Through the dynamic adjustment, DeepSeek-V3 keeps balanced expert load during training, and achieves better performance than models that encourage load balance through pure auxiliary losses.

10.4.4. MTP

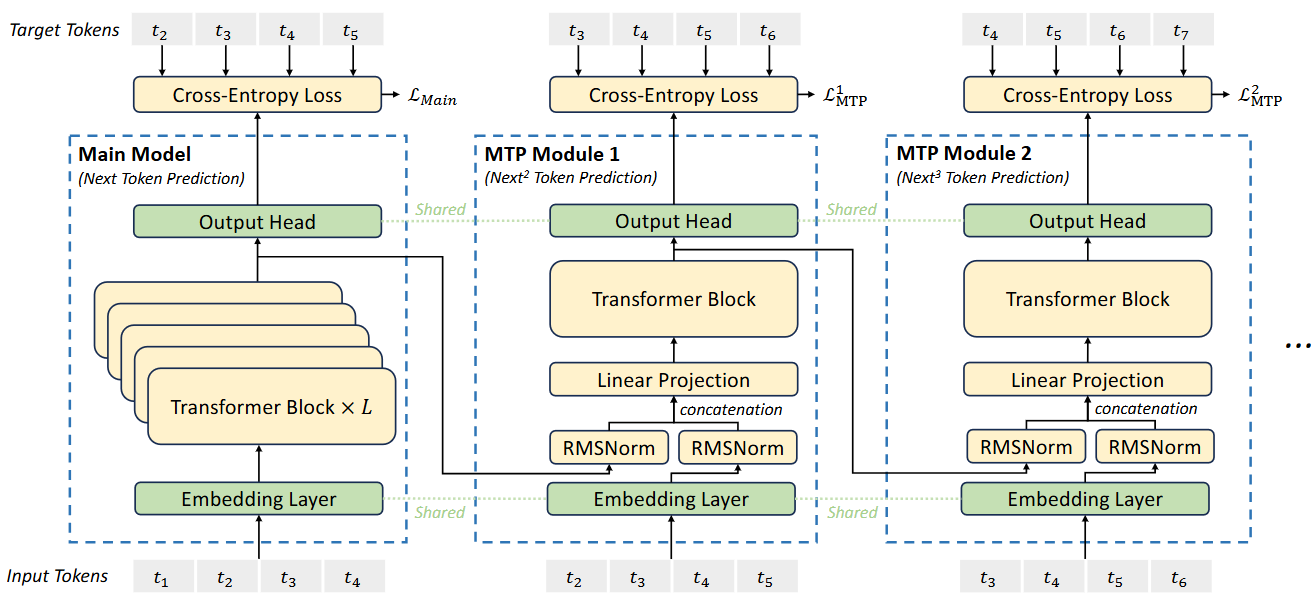
Fig. 10.6 Illustration of MTP architecture. Image from [DALF+24]

MTP Training Objective. For each prediction depth, we compute a cross-entropy loss \(\mathcal{L}_{\mathrm{MTP}}^k\) :

\[ \mathcal{L}_{\mathrm{MTP}}^k=\operatorname{CrossEntropy}\left(P_{2+k: T+1}^k, t_{2+k: T+1}\right)=-\frac{1}{T} \sum_{i=2+k}^{T+1} \log P_i^k\left[t_i\right], \]

where \(T\) denotes the input sequence length, \(t_i\) denotes the ground-truth token at the \(i\)-th position, and \(P_i^k\left[t_i\right]\) denotes the corresponding prediction probability of \(t_i\), given by the \(k\)-th MTP module. Finally, we compute the average of the MTP losses across all depths and multiply it by a weighting factor \(\lambda\) to obtain the overall MTP loss \(\mathcal{L}_{\text {MTP, }}\), which serves as an additional training objective for DeepSeek-V3:

\[ \mathcal{L}_{\mathrm{MTP}}=\frac{\lambda}{D} \sum_{k=1}^D \mathcal{L}_{\mathrm{MTP}}^k \]

MTP in Inference. Our MTP strategy mainly aims to improve the performance of the main model, so during inference, we can directly discard the MTP modules and the main model can function independently and normally. Additionally, we can also repurpose these MTP modules for speculative decoding to further improve the generation latency.

10.5. Bibliography

[DDZ+24]

Damai Dai, Chengqi Deng, Chenggang Zhao, RX Xu, Huazuo Gao, Deli Chen, Jiashi Li, Wangding Zeng, Xingkai Yu, Y Wu, and others. Deepseekmoe: towards ultimate expert specialization in mixture-of-experts language models. arXiv preprint arXiv:2401.06066, 2024.

[DALF+24] (1,2,3)

DeepSeek-AI, Aixin Liu, Bei Feng, Bing Xue, Bingxuan Wang, and others. Deepseek-v3 technical report. 2024. URL: https://arxiv.org/abs/2412.19437, arXiv:2412.19437.

[FZS22] (1,2)

William Fedus, Barret Zoph, and Noam Shazeer. Switch transformers: scaling to trillion parameter models with simple and efficient sparsity. Journal of Machine Learning Research, 23(120):1–39, 2022.